Voltage- and current-aware power constraints for BESSs in scheduling problems
Authors: Fabrizio Sossan, Stefano Cassano Last update: 29 March 2025
Energy management for batteries
When operating a Battery Energy Storage System (BESS), energy management is an essential task to ensure that the BESS has sufficient energy to provide the prescribed services. Energy management problems in the literature are commonly formulated as optimization problems, seeking to determine the optimal charging and discharging trajectories for the battery, based on forecasts of the services it is expected to deliver and subject to its power and state-of-charge constraints. This problem is also referred to as the scheduling problem.
Traditional formulation of BESS power constraints and an improved version
In such optimization problems, battery power constraints are typically formulated assuming that the battery can charge or discharge at the converter's rated power. Say $B_t$ is the battery power and $B_r$ the rated power of converter (and assuming, at this stage, no reactive power from the converter is involved in the problem), this reads as $-B^r \le B_t \le B^r$.
While this modeling choice leads to simple and easy-to-implement power constraints into optimization problems, it is also an approximation because the battery's charging and discharging capabilities depend on the current and voltage limits of the battery cells and are affected by the battery's State Of Charge (SOC). The following plot compares the static, "classic", power constraints (dashed lines) with the power constraints (continous lines) calculated accounting for the voltage and current limits of a large battery pack.
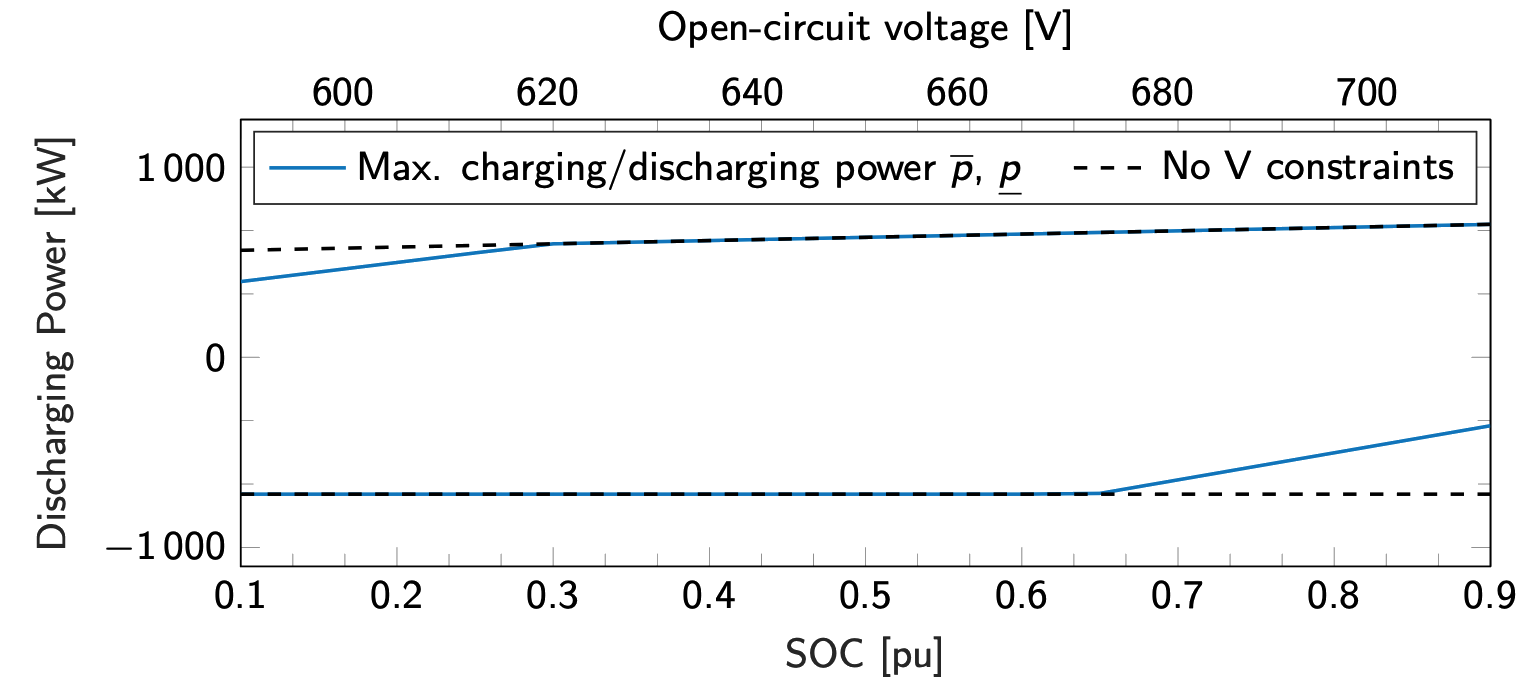
As the figure shows, the discharging power capability decreases when the battery is nearly empty (low SOC) due to the reduced internal battery voltage, which requires a higher current to deliver the same power. Conversely, the charging power capability is reduced when the battery is approaching 100% SOC because large charging currents might cause large voltage values. If you've ever used an electric vehicle (EV), you might have experienced these effects first-hand: when fast charging, the charging power slows down when the battery is nearly full, and when the battery is low, the car won't accelerate as fast.
The good news is that these more accurate power constraints are convex (and linear) with respect to the battery power, meaning you can implement them in your optimal scheduling problem without affecting its tractability. For more details, see the paper. In addition, many Model Predictive Control (MPC) strategies for batteries are built on similar principles, so these findings naturally extend to MPC and other forms of receding horizon optimization.
As a closing remark, while convexity may seem evident from the figure (the region enclosed by the blue line is indeed convex), there's more to consider given that, in a scheduling problem, the battery SOC is itself a function of the power. We have demonstrated convexity of the entire modeling toolchain (battery power to SOC to voltage- and to current-aware power constraints). This result follows from the fact that an affine transformation of a convex set preserves convexity. The only assumption necessary for this to hold is that the battery’s internal voltage and SOC are in a linear relationship, which is a reasonable approximation (except at extreme SOC levels).
What's the implication of using innacurate models of the battery power limits?
It’s important to note that, regardless of the charging or discharging power decision made by the scheduling problem or MPC, it is always the responsibility of the Battery Management System (BMS) to ensure that the selected power setpoint is feasible. From a safety perspective (a great concern for BESS), implementing innacurate power constraints in the decision-making model is thus not critical.
However, using inaccurate models for the power constraints can significantly degrade the performance of the scheduling action. For instance, the scheduler might unknowingly place the BESS in a state where it cannot deliver the required power; the BESS will thus fail in providing the service it was intended to deliver. This issue is especially critical in applications where BESSs are required to charge or discharge close to their rated power, in - what we call - power-intensive applications. Hydropower plants hybridized with BESS to reduce the fatigue of critical mechanical components (e.g., penstocks, turbines, guide vanes and associated mechanishms) is a prime example of such an application.
Complete formulation
For the complete formulation on how to formulate the SOC-dependant power capability curves of the BESS and how to derive convex power constraints for a BESS, please refer to the paper here below.